Modelos de sobrevivência no R

econometria

Autor

Alexsandro Prado

Data de Publicação

1 junho 2024

A Análise de Sobrevivência compreende os estudos em que o interesse principal é avaliar o tempo até a ocorrência de um evento pré-determinado. Esses tempos, chamados de tempos de falha, podem, então, ser explicados por outras variáveis a partir de modelos de regressão paramétricos ou semi-paramétricos. Uma característica fundamental desse tipo de estudo é a presença de censura, definida como a observação parcial do tempo de falha.

Para ilustrar as funções discutidas aqui, utilizaremos o banco de dados ovarian, do pacote survival. Este banco traz o tempo de sobrevivência (ou censura) de 26 mulheres com câncer de ovário e o objetivo do estudo foi comparar dois tratamentos distintos para essa doença.

Nesse exemplo, o tempo de falha é o intervalo entre a entrada no estudo e a ocorrência do evento de interesse que, aqui, é a morte da paciente. A censura neste caso é causada pelo abandono do estudo ou pela não ocorrência do evento até o fim do acompanhamento, ou seja, os casos em que a paciente estava viva no fim do estudo.

Para mais informações sobre o banco de dados, consulte o help(ovarian).

Kaplan-Meier e Log-rank

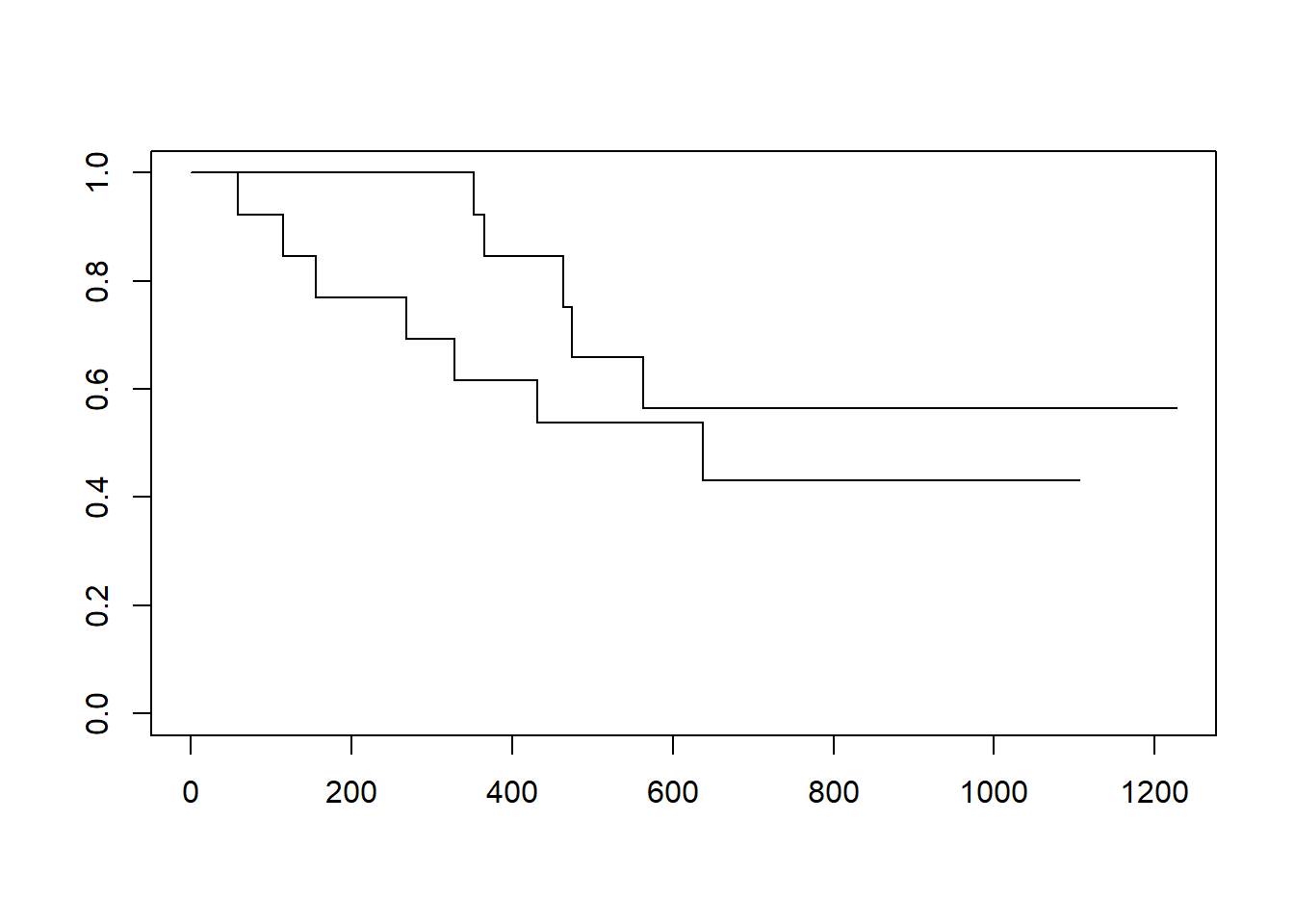
O Kaplan-Meier é a principal ferramenta para visualizar dados de sobrevivência. Esses gráficos ajustam curvas tipo-escada da proporção de indivíduos em risco — que ainda não falharam e não foram censurados — ao longo do tempo. Para plotar um Kaplan-Meier no R, utilizamos a função survfit() e a função plot().

Também podemos construir um Kaplan-Meier com o ggplot2, mas observe que é necessário fazer algums modificações no objeto fit:

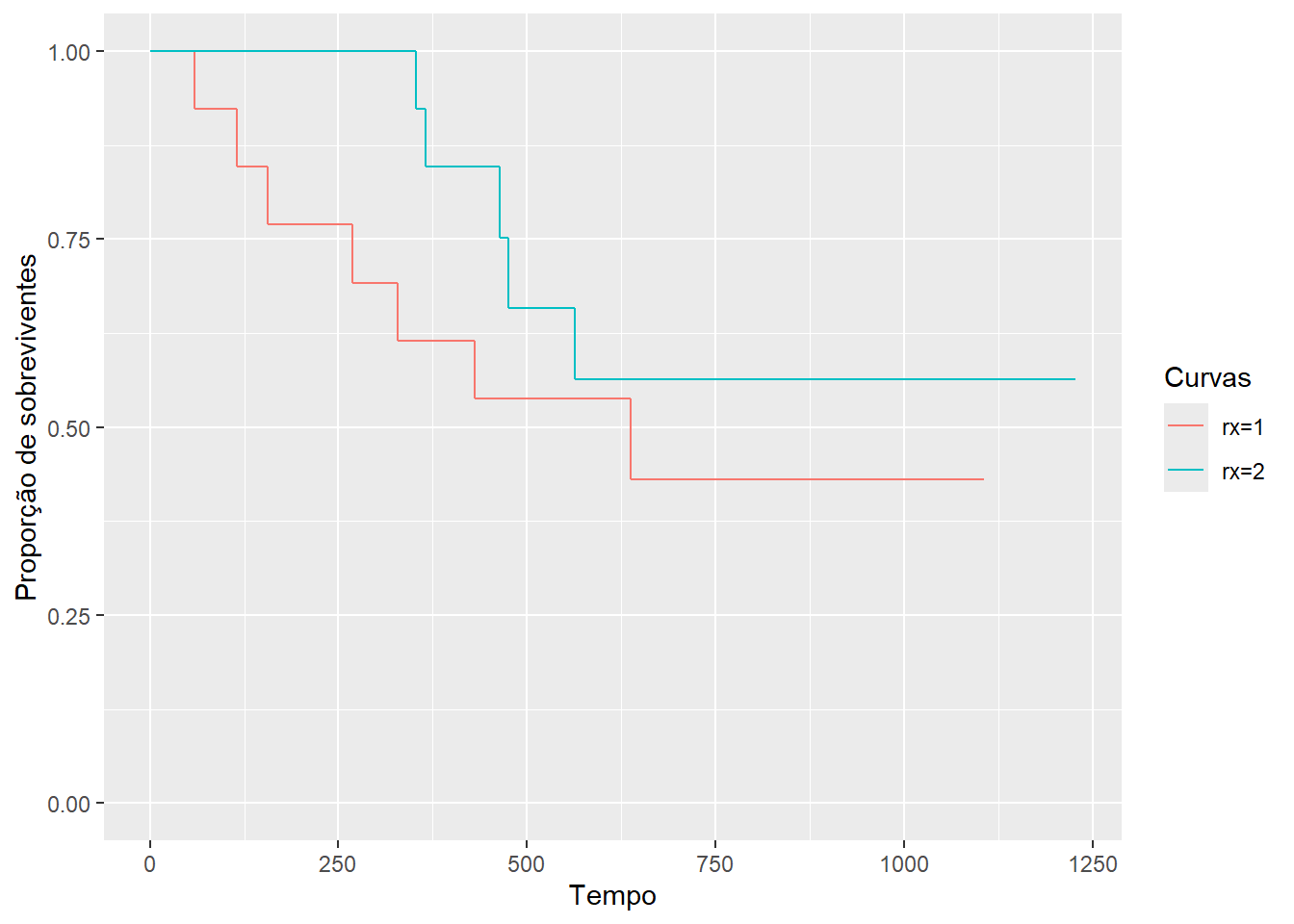
O teste de log-rank para comparação de grupos é realizado pela função survdiff():

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (O-E)^2/E (O-E)^2/V
rx=1 13        7     5.23     0.596      1.06
rx=2 13        5     6.77     0.461      1.06

 Chisq= 1.1  on 1 degrees of freedom, p= 0.3

Modelos paramétricos

Para ajustar modelos paramétricos, podemos utilizar a função survreg().


Call:
survreg(formula = Surv(futime, fustat) ~ rx + age, data = ovarian, 
    dist = "exponential")
              Value Std. Error     z       p
(Intercept) 12.1225     2.3966  5.06 4.2e-07
rx           0.6611     0.6159  1.07 0.28310
age         -0.1051     0.0319 -3.30 0.00098

Scale fixed at 1 

Exponential distribution
Loglik(model)= -91.2   Loglik(intercept only)= -98
    Chisq= 13.65 on 2 degrees of freedom, p= 0.0011 
Number of Newton-Raphson Iterations: 5 
n= 26

Observe que no exemplo acima utilizamos a distribuição Exponencial. O argumento dist = pode ser modificado para ajustarmos modelos com outras distribuições:

dist = "weibull" — distribuição Weibull (default)
dist = "gaussian" — distribuição Normal
dist = "logistic" — distribuição Logística
dist = "lognormal" — distribuição Log-normal
dist = "loglogistic" — distribuição Log-logística

Modelo semi-paramétrico de Cox

No R, a função mais utilizada para ajustar modelos de Cox é a coxph().

Call:
coxph(formula = Surv(futime, fustat) ~ age + rx, data = ovarian)

  n= 26, number of events= 12 

        coef exp(coef) se(coef)      z Pr(>|z|)   
age  0.14733   1.15873  0.04615  3.193  0.00141 **
rx  -0.80397   0.44755  0.63205 -1.272  0.20337   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

    exp(coef) exp(-coef) lower .95 upper .95
age    1.1587      0.863    1.0585     1.268
rx     0.4475      2.234    0.1297     1.545

Concordance= 0.798  (se = 0.076 )
Likelihood ratio test= 15.89  on 2 df,   p=4e-04
Wald test            = 13.47  on 2 df,   p=0.001
Score (logrank) test = 18.56  on 2 df,   p=9e-05

Generalized Additive Model (GAM)

Os modelos aditivos generalizados ou GAM são modelos baseados na teoria desenvolvida por Trevor Hastie e Robert Tibshirani, e podem ser vistos como uma generalização de GLM, no sentido de que todos os GLM sãoo casos particulares de GAM.

Na regressão normal e em GLM assumimos, em geral, que as variáveis aleatórias correspondentes aos indivíduos são independentes, e que existe uma função, denominada função de ligação, que une as médias destas variáveis aleatórias a um certo preditor linear.

A grande mudança nos modelos aditivos generalizados está na forma do preditor. Para cada variável explicativa, temos associada uma função a ser estimada (ou suavizada), sendo que o preditor fica definido como a soma dessas funções

g(\mu_i) = f_0 + \sum f(x_{ij})

Para evitar o desconforto da interpretação das contribuições marginais (funções), uma alternativa é utilizar as funções de suavização para ajustar variáveis de controle em que não há interesse direto, e manter a parte principal com termos paramétricos. Geralmente isso facilita a interpretação e melhora o ajuste do modelo em relação ao GLM.

Pacote mgcv

O pacote mgcv é um dos pacotes mais completos do R e permite simulação, ajuste, visualização e análise de resíduos para gam. O pacote gerou até um livro.

Na prática, a utilização do GAM não difere muito de modelos GLM. Uma das únicas diferenças na especificação do modelo é que podemos utilizar a função s para determinar quais termos queremos que sejam ajustados com funções aditivas.

Exemplo: PNUD


Family: Gamma 
Link function: inverse 

Formula:
espvida ~ ano + s(rdpc) + s(i_escolaridade)

Parametric coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.234e-01  1.545e-03   79.91   <2e-16 ***
ano         -5.437e-05  7.722e-07  -70.41   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                    edf Ref.df       F p-value    
s(rdpc)           8.858  8.993 1200.58  <2e-16 ***
s(i_escolaridade) 5.681  6.817   22.71  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.831   Deviance explained = 81.9%
GCV = 0.0011938  Scale est. = 0.001185  n = 16695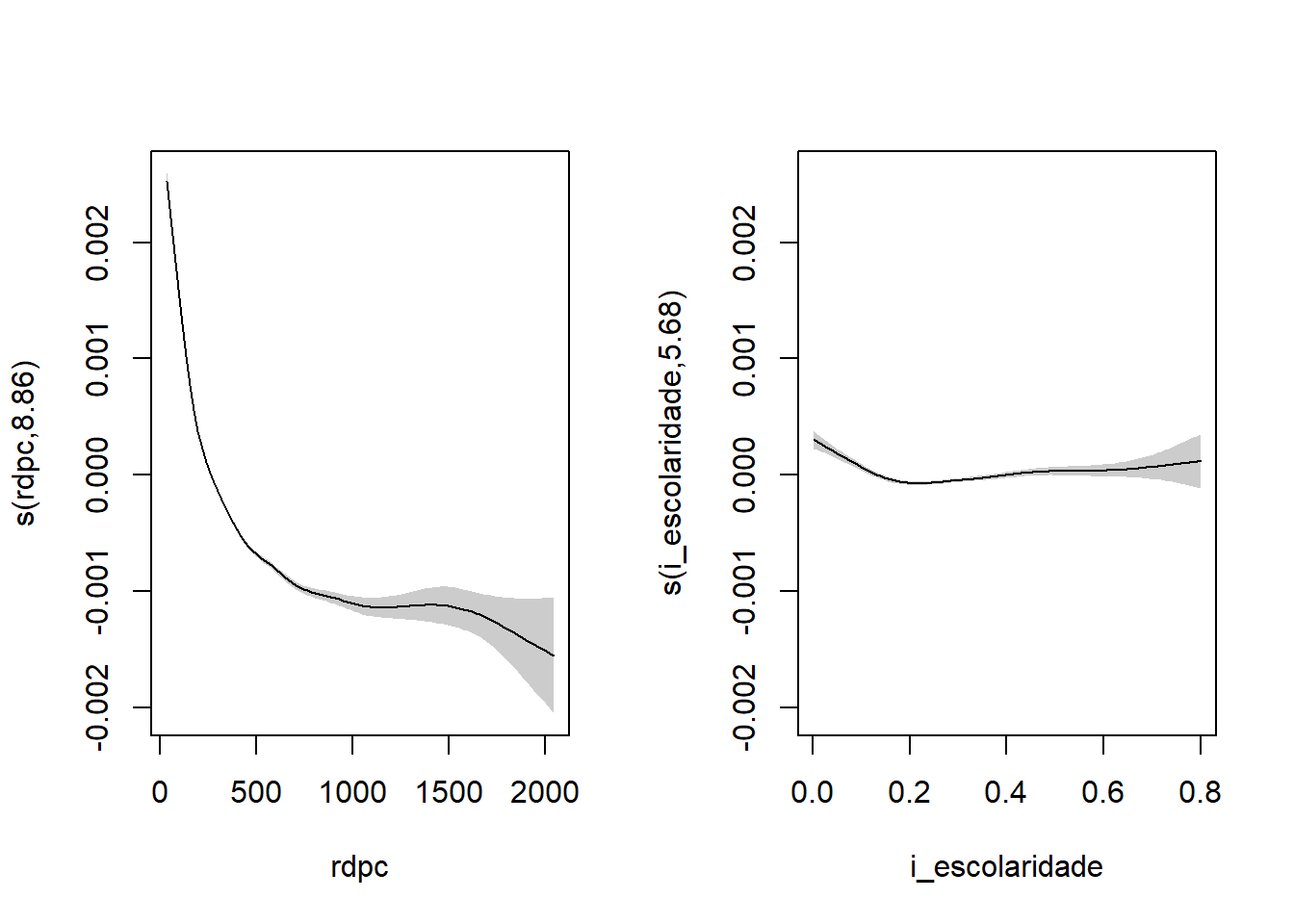

Pacote gamlss

Se por algum motivo existir algum problema na análise em relação à distribuição, heterocedasticidade, e utilização de preditores lineares, uma possível alternativa é o GAMLSS.

GAMLSS significa Generalized Additive Models for Location, Scale and Shape. Com GAMLSS é possível modelar não só a média da distribuição \mu_i (primeiro momento), mas também a variância \sigma_i (segundo momento), a assimetria \phi_i (terceiro momento) e a curtose \rho_i (quarto momento), usando preditores.

Por ser um modelo aditivo, o GAMLSS permite que sejam adicionados termos de suavização na fórmula do modelo, o que o torna uma generalização natural do GAM (em relação à modelagem, não ao método de ajuste).

Por fim, o modelo GAMLSS possui mais de 50 famílias de distribuições implementadas, o que nos dá uma enorme gama de opções para criação de modelos.

Também é possível adicionar efeitos aleatórios utilizando o GAMLSS, mas essa parte ainda é experimental.

Mas tudo vem com um preço. Por ser um grande canhão, o método de ajuste de modelos GAMLSS geralmente são baseados técnicas de otimização aproximadas. Além disso, o ajuste de modelos pode ser mais lento que os concorrentes. Por fim, a análise de resíduos para GAMLSS é bastante limitada (e provavelmente continuará sendo).

Recomendamos a utilização do gamlss com muito cuidado, e sempre acompanhando outras modelagens, usando glm ou gam, por exemplo.

Exemplo: PNUD

GAMLSS-RS iteration 1: Global Deviance = 78553.62 
GAMLSS-RS iteration 2: Global Deviance = 77935.35 
GAMLSS-RS iteration 3: Global Deviance = 77903.36 
GAMLSS-RS iteration 4: Global Deviance = 77900.75 
GAMLSS-RS iteration 5: Global Deviance = 77900.38 
GAMLSS-RS iteration 6: Global Deviance = 77900.32 
GAMLSS-RS iteration 7: Global Deviance = 77900.31 
GAMLSS-RS iteration 8: Global Deviance = 77900.31 
GAMLSS-RS iteration 9: Global Deviance = 77900.31

******************************************************************
Family:  c("NET", "Normal Exponential t") 

Call:  gamlss(formula = espvida ~ cs(rdpc) + cs(i_escolaridade),  
    sigma.formula = ~ano, family = NET(), data = dados) 

Fitting method: RS() 

------------------------------------------------------------------
Mu link function:  identity
Mu Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)        6.072e+01  4.392e-02 1382.42   <2e-16 ***
cs(rdpc)           1.150e-02  1.201e-04   95.71   <2e-16 ***
cs(i_escolaridade) 1.556e+01  1.958e-01   79.46   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Sigma link function:  log
Sigma Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.11223    0.01309   85.00   <2e-16 ***
ano2000     -0.34429    0.01745  -19.73   <2e-16 ***
ano2010     -0.76936    0.01808  -42.56   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

------------------------------------------------------------------
Nu parameter is fixed 
Nu =  1.5 
------------------------------------------------------------------
Tau parameter is fixed 
Tau =  2 
------------------------------------------------------------------
NOTE: Additive smoothing terms exist in the formulas: 
 i) Std. Error for smoothers are for the linear effect only. 
ii) Std. Error for the linear terms maybe are not accurate. 
------------------------------------------------------------------
No. of observations in the fit:  16695 
Degrees of Freedom for the fit:  28.32315
      Residual Deg. of Freedom:  16666.68 
                      at cycle:  9 
 
Global Deviance:     77900.31 
            AIC:     77956.95 
            SBC:     78175.69 
******************************************************************

******************************************************************
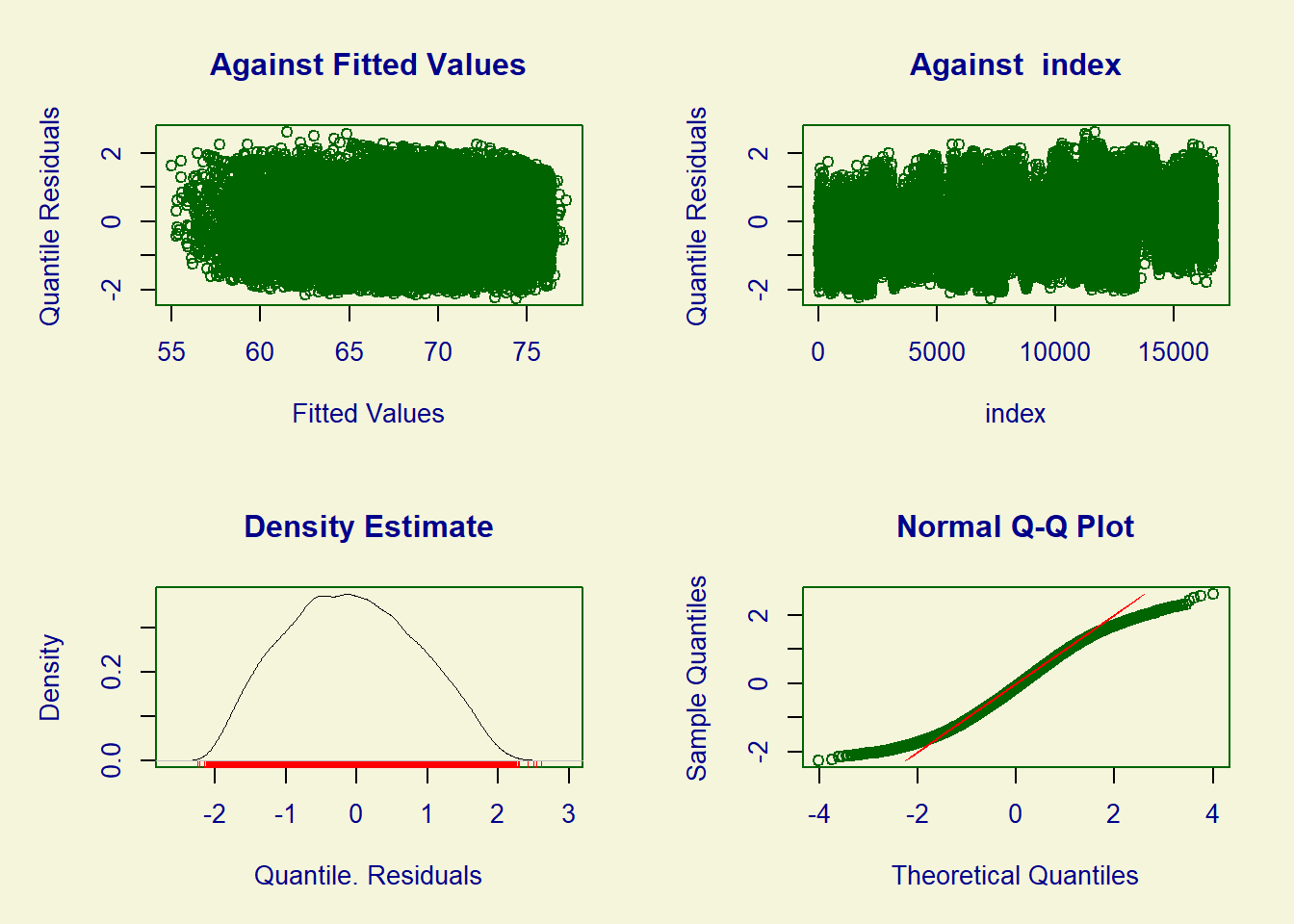
          Summary of the Quantile Residuals
                           mean   =  -0.08278299 
                       variance   =  0.8508743 
               coef. of skewness  =  0.1034363 
               coef. of kurtosis  =  2.249083 
Filliben correlation coefficient  =  0.9937856 
******************************************************************

Para mais informações sobre Análise de Sobrevivência, consultar as seguintes referências:

Colosimo, E.A. e Giolo, S.R.. (2005) Análise de Sobrevivência Aplicada. ABE — Projeto fisher. Editora Edgard Blucher
Kalbfleisch, J. D.; Prentice, Ross L. (2002). The statistical analysis of failure time data. New York: John Wiley & Sons.
Lawless, Jerald F. (2003). Statistical Models and Methods for Lifetime Data (2nd ed.). Hoboken: John Wiley and Sons.

Referências

CURSO-R. curso-r.github.com. Disponível em: https://github.com/curso-r/curso-r.github.com/. Acesso em: 02 jun. 2024.

De volta ao topo